آیا شما از خالی و بی نقش بودن دیوار خانه ی خود خسته شده اید؟ شما میتوانید به سادگی این دیوار ها را تزئین کنید ، با وسایل ساده بپوشانید و خلاقیت خود را بر روی دیوارها پیاده کنید. همانطور که شما دوست دارید لباس های شیک یپوشید تا جذاب به نظر برسید میتوانید دیوارهای خانه ی خود را نیز با اثرات هنری بپوشانید. پروژه هنر دیواری به پیدا کردن، ایده دکوراسیون دیوار و تصورات که می تواند استعداد و سبک برای فضاهای تان به ارمغان بیاورد ، کمک کند. فراتر از الهام، شما همچنین می توانید از طرح های هنر دیوار ایده های
فراتر از الهام، شما همچنین می توانید ایده های طرح های هنر دیواری که به شما برای تزئین دیوارتان و همچنین اویختن کار هنری خود در جای مناسب کمک میکند را پیدا کنید.
ایده هنر دیواری شما باید سبک و شخصیت را به اتاق شما اضافه کند. شما باید بتوانید با صرف هزینه های کمک کارهای هنری و خلاقانه در اتاقتان انجام دهید.
ما در اینجا ایده های دکوراسیون دیوار که به شما در تزئین دیوار منزلتان کمک میکند برای شما آورده ایم. طرح های مختلف که بزرگسالان همانند کودکان آنها را می پسندند. مانند سبک هنر دیواری پروانه ای، سبک ماهی،سبک پرندگان و ….
با ما همراه باشید با ایده هایی که برای تزئین و دکوراسیون دیوار شما گرد آوری کرده ایم:
۱٫ استفاده از جعبه و ایجاد تابلو به شکل قلب
این طرح مربوط به طرح قلب با سبک متفاوت می باشد. شما می توانید از جعبه های مقوایی برای ساخت یک تابلو و یا یک ساعت به شکل قلب استفاده کنید و فضای اتاق خود را رومانتیک کنید.
۲٫ هنر دیواری از بوم نقاشی DIY
شما میتوانید از بوم نقاشی خود برای هنر دیواری DIY استفاده کنید. شما میتوانید نقاشی های خود را در شیوه ها و سبک های شیک و مختلف به دیوار آویزان کنید. شما فقط به یک تابلو، تعدادی چوب بامبو، و طناب نیاز درید. این طرح خیلی زیبا و چشمگیر به نظر می آید.
۳. ایده دکوراسیون دیوار پروانه ای
این طرح بیشتر برای اتاق نشیمن استفاده می شود. این سبک مانند استفاده از کاغذ دیواری ساده می باشد. شما میتوانید از کیفیت بالا برای دادن یک جلوه ی خوب و خلاقانه به دیوار خود استفاده کنید.

۴٫ طرح هنر دیواری اشکال هندسی
با این طرح یک ظاهر متفاوت و منحصر به دیوار اتاق خود بدهید. این طرح از اشکال هندسی که بسیار آنتیک هستند ایجاد شده است. این سبک یک جلوه ایده آل به دیوار اتاق شما می دهد.
۵٫ طرح هنر دیواری قلب رشته ای
این طرح عمدتا از کاموا و آرایش مناسب میخ ها ساخته می شود. بهتر است از کاموا به رنگ قرمز که نشانه ای از عشق است استفاده کنید. نمونه ای از این طرح زیبا و خلاقانه را در زیر مشاهده کنید.

۶٫ طرح هنر دیواری آینه ی خورشیدی
این طرح به اتاق خواب و اتاق مهمان شما ظاهر بسیار شیکی می دهد. این طرح ، سبک اتاق شما را به طور کامل تغییر می دهد. این اثر هنری میتواند به وسیله ی چوب های جمع شده و وصل کردن آنها به شکل خورشید ساخته شود.
۷٫ ایده های هنر دیواری کاغذ دیواری و پس زمینه اتاق
این طرح رنگارنگ بسیار جذاب و مدرن می باشد. این طرح توسط تعدادی کاغذ رنگی و چسباندن آنها به دیوار ایجاد می شود. در این طرح اگر از رنگ های روشن استفاده کنیم زیباتر می گردد.

۸٫ طرح هنر دیواری سیمی
در این طرح از سیم برق و شکل دادن آن در الگوهای مختلف استفاده می گردد. این ایده بسیار کم هزینه است و در عین حال جلوه ی بسیار زیبا و شیکی دارد.

۹٫ هنر مهارت و خلاقیت
این ایده یک پروژه هنری دیواری است که به طور عمده از وسایل خانگی که بسیار جذاب و الهام بخش به نظر می آیند ساخته می شوند. شما میتوانید با این سبک اتاق تان را به یک اتاق رویایی و زیبا تبدیل کنید.

۱۰٫سبک مونوگرام
هر زمان که ما به تزئین دیوار خود فکر کنیم ایده های بسیاری به ذهن ما خطور می کنند. اگر از این ایده ها به درستی استفاده شوند نتایج بسیار عالی خواهند داشت.
۱۱٫ هنر دیواری پوست ماهی
این طرح دکوراسیون و تزئین دیوار با هر چیری که به ماهی مرتبط باشد، ایجاد می شود. این طرح ساده و در عین حال زمان بر می باشد. این طرح را میتوانید در تعطیلات آخر هفته ی خود انجام دهید.

۱۲٫ ایده تزئین دیوار با بنر نخی
این طرح ساده می باشد و به دلیل استفاده از نخ در رنگ های مختلف، جلوه ی شیک و رنگارنگی دارد. شما میتوانید تمام نخ هایی که اضافه مانده اند جمع آوری کنید و سپس آنها را برای جلوه دادن به دیوار اتاق خود مرتب کنید.
۱۳٫طراحی دیوار الهام بخش
کودکان شما مطمعنا اسباب بازی های بی استفاده ، بازی حروف و .. دارند.از این اسباب بازی ها میتوان در تزئین اتاق کودکان استفاده کرد. نمونه ای از این ایده خلاقانه را در زیر مشاهده کنید.
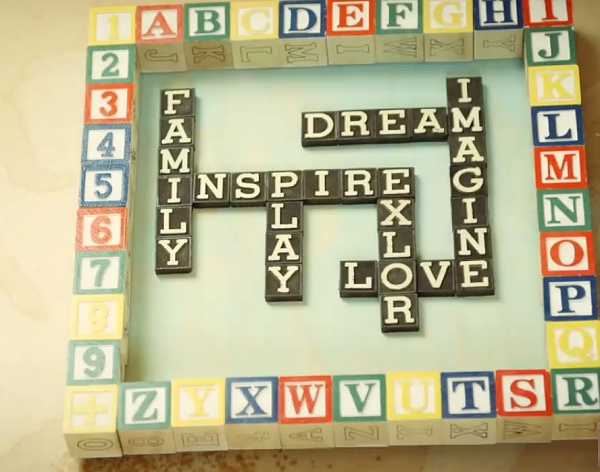
۱۴٫هنر دیواری قاب سی دی
شما مطمعنا این طرح را دوست دارید چون این طرح بسیار چشمگیر است و جلوه ی زیبایی به دیوار اتاق شما می دهند. این طرح به وسیله ی کاغذ های رنگی بی استفاده که مناسب و معقول به نظر می آیند ساخته می شوند.

۱۵٫هنر دیواری پالت
این طرح طرحی خوب و منحصر به فرد می باشد. این طرح با استفاده از پالت های مختلف برای تزئین دیوار ایجاد می شود.

۱۶٫هنر دیواری چوب های بی استفاده
این سبک شیک ریشه های سنتی دارد. دیوار خود با استفاده از تصورات ذهنی خود ظاهری متفاوت بدهید. در این سبک از چ.ب های وسایل چوبی که خراب شده اند، استفاده می شود.

۱۷٫تابلوهای چوبی با طرح های توخالی
این طرح عمدتا در مناطق خاص خانه استفاده می شوند. مثلا میتوان از طرح چاقو، چنگال و قاشق برای آشپزخانه خود استفاده کنید. این تابلو یک جلوه متفاوت و شایان ستایش به آشپزخانه شما می دهد.

۱۸٫ طرح هنری اتاق خواب DIY
طرح ها برای اتاق خواب دوست داشتنی شما موجود می باشند که به اتاق خواب شما یک سبک منحصر به فرد و تازه و مدرن می بخشد.

۱۹٫طرح های هنری دیواری DIY
میتوانید تعدادی دکمه جمع آوری کنید و آنها را به صورت اشکال مختلف در کنار هم بچینید.
۲۰٫ طرح های دیواری هنری و ماهرانه
این طرح بسیار منحصر به فرد و مقرون به صرفه می باشد.این طرح را میتوان با استفاده از هر وسیله ای مه در دسترس دارید بسازید.

۲۱-هنر دیواری پزوانه های کاغذی سه بعدی
شما میتوانید با استفاده از این پروانه ها سبک ها و ایده های مختلفی بر روی دیوار خود پیاده کنید. این طرح به دیوار شما یک جلوه ی شاد و فرح بخش می بخشد.
 شما میتوانید با استفاده از این طرح ها و ایده های ارائه شده دیوار اتاق کسل کننده و بی روح اتاق خود را به یک دیوار شاد و خلاقانه تبدیل کنید.
شما میتوانید با استفاده از این طرح ها و ایده های ارائه شده دیوار اتاق کسل کننده و بی روح اتاق خود را به یک دیوار شاد و خلاقانه تبدیل کنید.
ایده های خلاقانه برای دکوراسیون منزل/ایده های خلاقانه برایتزئین دیوار/ایده های خلاقانه و جالب/ایده های خلاقانه در منزل/خلاقیت در منزل با وسایل ساده/خلاقیت در تزیین دیوار/ایده های خلاقانه با وسایل دور ریختنی/خلاقیت در منزل با وسایل دور ریختنی/ایده های خلاقانه و ارزان برای تزیین دکوراسیون منزل, روش های تزیین و زیبا کردن خانه/یده های جالب دکوراسیون,ایده های جالب برای دکوراسیون داخلی,ایده های خلاقانه ای که هزینه چندانی ندارند/ ایده هایی زیبا برای تزیین دیوار/استفاده از جعبه در دکور /ایده تزیین دیوار/ ایده خلاقانه/ ایده ساخت قفسه/ ایده های دکوراسیون/ ایده های هنری / ایده های خلاقانهتزیین دیوار /تزیین دیوار با وسایل ساده …
منبع: http://mehrmihan.ir/creative-ideas-for-wall-decoration/




































![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/93_20131611505080a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/56_20131611505072a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/54_20131611505143a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/5_20131611505184a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/30_20131611505185a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/4_20131611505136a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/77_20131611505167a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/2_20131611505158a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/19_20131611505169a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/63_201316115051810a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/33_201316115051611a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/37_201316115051412a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/83_201316115051513a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/30_201316115051614a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/32_201316115051615a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/36_201316115051816a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/72_201316115051717a,33584.jpg)
![گالری عکس کودک (27) ,[categoriy] child-photo](http://mehrmihan.ir/wp-content/uploads/97_201316115051318a,33584.jpg)

















































,22097.jpg)
,22097.jpg)





